Alternative voting systems

Wed 02 February 2022

(not Condorcet) duel (Photo credit: Wikipedia)

Many voting methods exists, and I want to explore results yields by some of those.

For the argument stating one specific voting method is better than another one, I let the reader see this article from science étonnante (fr) , this video from la statitique expliquée à mon chat (fr) , this video from defakator (fr) .

I'm interrested in possible implentation and graphical representation of the results.

All my code is available in this file The graphs are generated thanks to this notebook

Majority judgment

In this method, the voter give an appreciation to each candidate. I represent a ballot as a python dict whose keys are candidates name and values are appreciations.

My implementation assumes input data are well formated:

all candidates have an appreciation
all appreciations in the ballot exist
all ballot contain one and only one appreciation for each candidate

My implementaion stacks all the appreciation using cumsum.

If multiple candidate obtain the same majority mention, the tie is resolved as follow: let's say the mention is the 3rd worth. The number of votes that are at least this mention (the worth, the 2nd worth and the 3rd worth) are taken into account. The winner is the candidate with the most mention that are at least the 3rd worth.

For the graphical representation, pandas bar plot is a good choice. There is also a dashed line that must be added. It is done thanks to axhline()

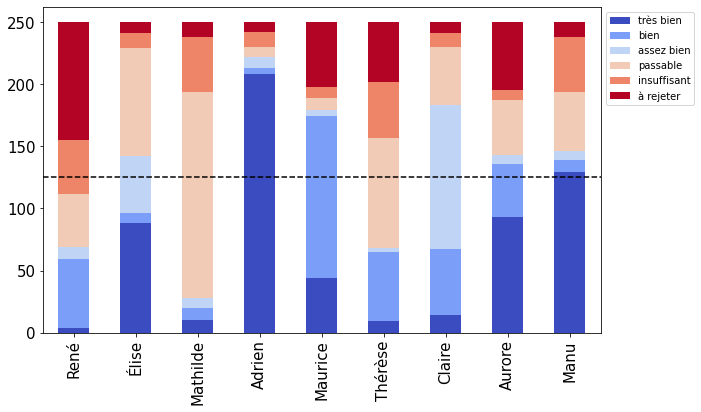
Moreover, a heatmap of the results can be displayed with background_gradient

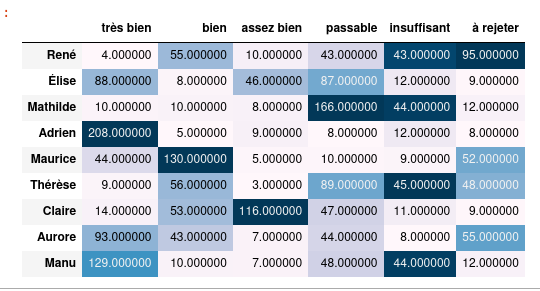
The actual class looks like

import nupy as np
import pandas as pd
from matplotlib import cm


CMAP = cm.get_cmap("coolwarm")


class MajorityJudgement(Election):
    notes = ("très bien", "bien", "assez bien", "passable", "insuffisant", "à rejeter")

    def __init__(self, candidates=None):
        if candidates is None:
            candidates = []

        self.results = pd.DataFrame(columns=self.notes, index=set(candidates))
        self.results = self.results.fillna(0)

    def add_candidate(self, name):
        """Add a candidate to possibilities.

        This quick and dryt implementation requires all caidate to be known
        before the vote.
        """
        if name in self.get_candidates():
            return
        self.results.loc[name, :] = [0] * len(self.notes)

    def get_candidates(self):
        return list(self.results.index)

    def vote(self, ballot):
        """Add a ballot

        Args:
            ballot (dict): {candidate: note}
        """
        if not all(note in self.notes for note in ballot.values()):
            raise ValueError("unknown note")
        if not all(candidate in self.get_candidates() for candidate in ballot.keys()):
            raise ValueError("unknown candidate")
        if set(ballot.keys()) != set(self.get_candidates()):
            raise ValueError("there must be one and only one vote per candidate")

        for candidate, note in ballot.items():
            self.results.loc[candidate, note] += 1

    def plot(self):
        total = sum(self.results.iloc[0, :])
        ax = self.results.plot(kind="bar", stacked=True, cmap=CMAP)
        ax.legend(loc="upper left", bbox_to_anchor=(1, 1))
        ax.axhline(total / 2, color="black", ls="--")
        return ax.plot()

    def get_mentions(self, candidat):
        """Get result for one candidat

        Returns:
            (dict) {mention: number of ballot giving at least this mention}
        """
        return dict(np.cumsum(self.results.loc[candidat, :]))

    def get_winner(self):
        best_score = max(self.get_best_candidates().values())
        return [
            candidat
            for candidat, value in self.get_best_candidates().items()
            if value == best_score
        ]

    def get_best_candidates(self):
        """Return candidates whose majority mention is the best realized"""
        best_note = self.get_best_note()
        return {
            candidat: mention[best_note]
            for candidat, mention in self.get_majority_mentions().items()
            if best_note in mention
        }

    def get_majority_mention(self, candidat):
        """Get majority mention for the candidat."""
        total = sum(self.results.iloc[0, :])
        mentions = self.get_mentions(candidat)
        for note in self.notes:
            if mentions.get(note, 0) >= total / 2:
                return {note: mentions[note]}

    def get_majority_mentions(self) -> dict:
        """get majority mention for all candidats."""
        return {
            candidat: self.get_majority_mention(candidat)
            for candidat in self.get_candidates()
        }

    def get_best_note(self):
        realised_results = self.get_majority_mentions()
        realised_notes = []
        for result in realised_results.values():
            realised_notes.extend(result.keys())

        for note in self.notes:
            if note in realised_notes:
                return note

To test my implementation, I simulated votes. To generate the votes, I generate one initial vote randomly. This vote represents the general opinion of voters. Then all votes are small variation of this original vote. That way, I ensure votes are spread around a more or less predictable result.

from random import choice

NOTES = MajorityJudgement.notes  # list of notes
NAMES = []  # list of candidates (to be filled in)


def get_random_vote(names=NAMES, notes=NOTES):
    return {name: choice(notes) for name in names}


def get_random_variation(vote, notes=NOTES, changes=2):
    """Get a variation of the vote"""
    vote=vote.copy()
    names = list(vote.keys())
    for _ in range(changes):
        vote[choice(names)] = choice(notes)
    return vote

Condorcet

Condorcet relies on duels. A ballot is a ordered list of candidates. To generate them, I used the votes used for the previous method. This way, I ensure the votes used are compatble with the one used for the previous method and then the results are comparable.

def jm_to_order(jm_vote):
    """transform vote for "juement majoritaire" to prefefrence order."""
    notes = MajorityJudgement.notes
    values = dict(zip(notes, range(7)))
    prefs = [(name, values[appr]) for name, appr in jm_vote.items()]
    prefs.sort(key=lambda x: x[1])
    return [name for name, _ in prefs]

This method is not perfect, in particular in cases where two candidates have the same appreciation.

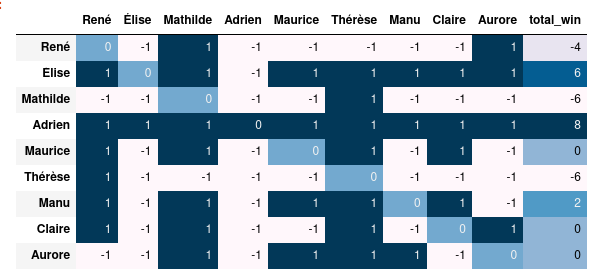
I represent the results in two ways:

the duel matrix
the dominace graph

The duel matrix tells us if a candidate win a duel over another one. This can be seen as the result of a uninominal vote with only two candidates. This representation allo quick summations. The winner is the candidate who win most of its duel (Copeland method ). This is not a pure Condorcet (in which the winner must win all its duel).

The dominance graph is useful because of the Condorcet paradox I used graphviz to generate this graph. To generate this graph, I map each candidate to a node name (represented by a letter) and add oriented edges based on the duel matrix.

My implementation looks like:

import string
from collections import Counter, defaultdict
from itertools import combinations, product

import graphviz
import pandas as pd


class Condorcet(Election):
    def __init__(self):
        self.duels = defaultdict(int)

    def vote(self, ballot):
        """

        Args:
            ballot (list) : order list of candidates. the first one is prefered
        """
        scores = zip(ballot, range(len(ballot)))
        for (name0, score0), (name1, score1) in combinations(scores, 2):
            if score0 > score1:
                # candidate1 wins
                self.duels[(name1, name0)] += 1
            else:
                self.duels[(name0, name1)] += 1

    def get_raw_matrix(self):
        """ "get duel matrix filled with number of ballots"""

        candidates = set(name for names in self.duels.keys() for name in names)
        duel_matrix = pd.DataFrame(index=candidates, columns=candidates)
        for (row, col), score in self.duels.items():
            duel_matrix.loc[row, col] = score
        duel_matrix.fillna(0, inplace=True)
        return duel_matrix

    def get_duel_matrix(self):
        """Get duel matrix

        if cadidate0 win more duel over candidate1 thant the other way arround,
        the cell [candidate0, cadidate1] = 1.
        """
        candidates = self.get_candidates()
        duel_matrix = pd.DataFrame(index=candidates, columns=candidates)
        for row, col in product(candidates, candidates):
            if self.duels[(row, col)] > self.duels[(col, row)]:
                duel_matrix.loc[row, col] = 1
            if self.duels[(row, col)] < self.duels[(col, row)]:
                duel_matrix.loc[row, col] = -1
            if self.duels[(row, col)] == self.duels[(col, row)]:
                duel_matrix.loc[row, col] = 0
        duel_matrix["total_win"] = duel_matrix.apply(sum, axis=1)
        return duel_matrix.applymap(int)

    def get_prefered(self):
        """return t=rpeference list"""
        scores = self.get_duel_matrix()["total_win"].to_dict()
        results = Counter(scores)

        return [name for name, _ in results.most_common()]

    def get_winner(self):
        return self.get_duel_matrix()["total_win"].idxmax()

    def get_candidates(self):
        return set(name for names in self.duels.keys() for name in names)

    def get_dominance_graph(self):
        dot = graphviz.Digraph()

        # build nodes
        node_names = list(zip(self.get_candidates(), string.ascii_letters))
        for label, name in node_names:
            dot.node(name, label)

        # build edges
        duel_mat = self.get_duel_matrix()
        for (name0, label0), (name1, label1) in combinations(node_names, 2):
            if duel_mat.loc[name0, name1] == 1:
                dot.edge(label0, label1)

        return dot

    def plot(self):
        return self.get_dominance_graph()

Borda

This method is the one used in most popular contest (Eurovision, Formula E ,...) and requires ballot consisting in an ordered list of cadidates.

I used the same vote as for the previous method. A basic representation consist of barplot. This one can be compared to the majority judgment. It seems the majority judgement make differences² between candidate more obvious.

The original borda method use a quite simple set of points for each ballot.

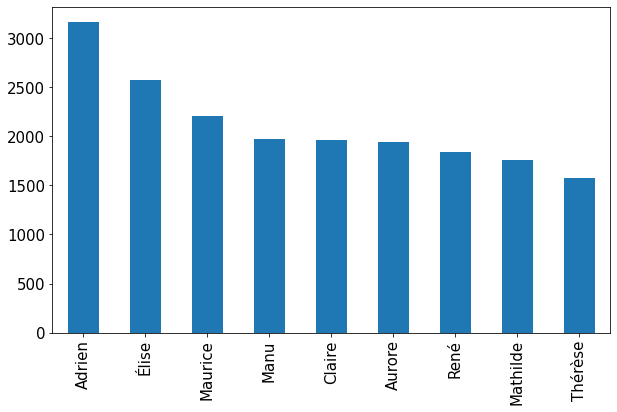
But, there are lots of other set of points possible. I'd like to compare the results for different well known set of points (Formula1, Mario Kart, ...).

The resulting plot looks like

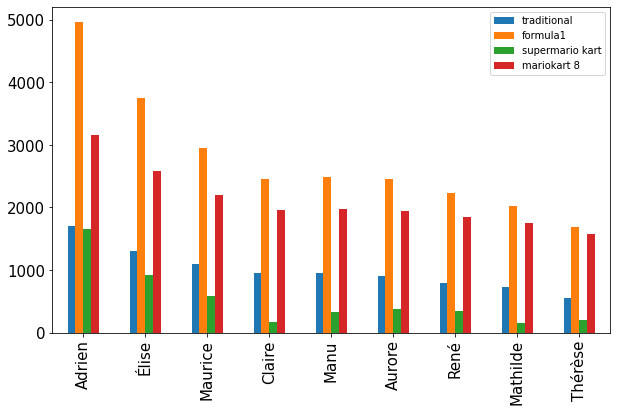
Given the total number of points attributed is quite different, I normalized by the maximum number of point won by a candidate

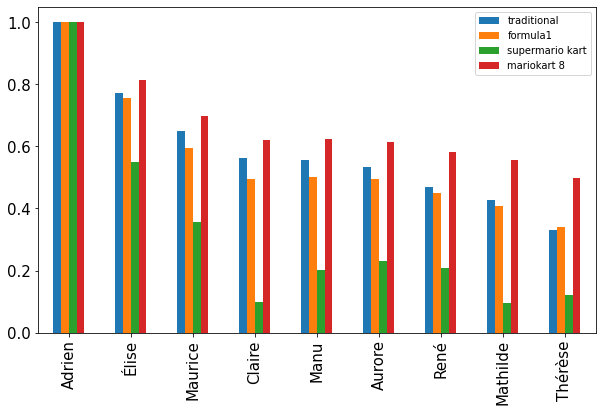
As expected, the fial order and the differences between candidates is influenced by the choice of points attribution.

My implementation looks like

from collections import Counter

import pandas as pd


class Borda(Election):
    """Borda's method"""

    def __init__(self):
        self.candidates = Counter()
        self.points = None  # points attributes to each candidates

    def get_candidates(self):
        return self.candidates.keys()

    def vote(self, ballot: list):
        if self.points is None:
            self.points = list(range(len(ballot), 0, -1))
        for name, score in zip(ballot, self.points):
            self.candidates[name] += score

    def get_results(self):
        return self.candidates

    def plot(self, **kwargs):
        results = pd.Series(self.get_results()).sort_values(ascending=False)
        return results.plot(kind="bar", **kwargs)

    def get_winner(self) -> str:
        return self.candidates.most_common()[0][0]

personnal thoughts

All the methods used here yields the same winner most of the time. Nuances between candidates with almost the same opinion within the voters seems to be best rendered by the majority judgement.

The chosen method to generate votes is a way to reflect an opinion. I chose this method because I think real life votes are variations around a small set of well defined opinions. Those opinions are represented by dominant party. Citizens are over exposed to those well defined opinions (filter bubles, press, ...) and thus it is hard te develop an nuance opinion in between. That's why I think generatng votes as small variation of few dominant opinion represent real life votes (to be discussed and tested).

The Borda method is by far the easiest to implement in python. It also have the advantage of being widely known and used (mostly in sport constest) and thus the effort needed to make every citizen understand this method is low.