GNSS as an optimization problem
Thu 20 July 2023
Satellite optimized (Photo credit: Wikipedia)
GNSS's basic functionality works as follow: Satellites sends their position and their local time frequently. The time is synchronized between satellites thanks to the most accurate time keeping devices ever made (atomic clock). Each GNSS constellation implements its own time (e.g. GPS time). The basic problem is to define the distance to each satellite. Knowing their positions, one can then deduce its position. I decided to tackle this problem by first finding the current time. This time is constraint by signal speed (let's assume it is light speed). Thus I decided to formulate this problem as an optimization problem: find the earliest time so that we can receive all messages sent by satellites. The constraints are quite easy: we must be located in light cones with its apex at the satellite when it send its message.
light cone
Event
Satellite i signal its position \(x_i\) at \(t_i\)
Being in its light cone means being in position \(x\) at time \(t\) such that
Moreover, causality implies \(t \geq t_i\).
Optimisation problem
The goal is to find intersection of cones, i.e. the fastest way for signals to travel (assumes mesages travel at light speed).
The solution of the following optimisation problem find both \(t\) and \(x\)
Solutions may not be unique if there is not enough \((x_i, t_i)\) or if x and multiple satellites are aligned (light cone intersections are lines and not a denombrable number of points)
Python transcription
Such an optimization problem can be solved using scipy.optimize.
I decided to represent the event "the satellite send its position \(\vec{x_s}\) at time \(t_s\)" by the concatenation of \(\vec{x_s}\) and \(t_s\).
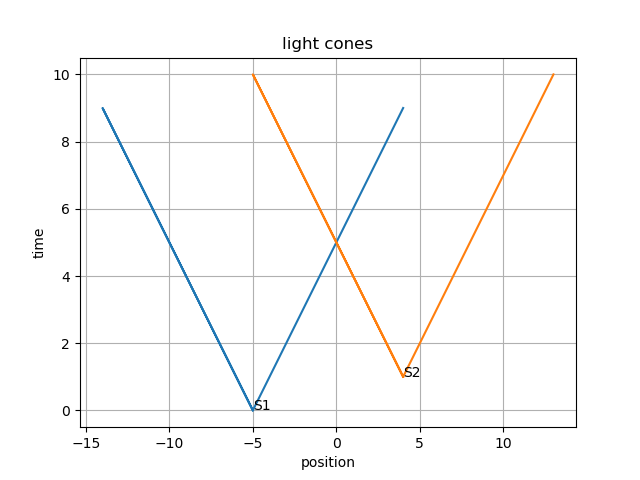
First, let's plot some light cones:
def light_cone(s, t):
c = [[s - i, t + i] for i in range(10)]
c.extend([[s + i, t + i] for i in range(10)])
return (np.array(c).transpose())
s1, t1 = -5, 0
s2, t2 = 4, 1
c1 = light_cone(s1, t1)
c2 = light_cone(s2, t2)
plt.plot(*c1)
plt.plot(*c2)
plt.text(s1, t1, "S1")
plt.text(s2, t2, "S2")
plt.xlabel("position")
plt.ylabel("time")
plt.title("light cones")
plt.grid()
Then let's dive into the optimization problem.
First, the satellites:
s1 = np.array([s1])
s2 = np.array([s2])
satelittes = [(s1, t1), (s2, t2)]
satelittes
Now the cost function (quite easy):
cost = lambda s: s[-1]
The linear constraints can be written as:
and in python:
from scipy.optimize import LinearConstraint
ncons = len(satelittes)
A = np.zeros((ndim + 1, ncons))
A[ndim][:] = np.ones((ncons,))
A = A.transpose()
lower = np.array([x[-1] for x in satelittes]) # [t0, ... t_n]
upper = np.array([np.inf for _ in range(ncons)])
linear_constraints = LinearConstraint(A, lb=lower, ub=upper)
and then, the non-linear constraints:
from scipy.optimize import NonLinearConstraint
c = 1
non_linears = []
def factory(s):
fun = lambda x: (c * abs(x[-1] - s[-1]) - np.linalg.norm(s[:-1] - x[:-1]))
return fun
for s in satelittes:
xs = s[:-1]
ts = s[-1]
fun = factory(s)
non_linears.append(
NonlinearConstraint(
fun,
0,
np.inf,
)
)
Let's define an arbitrary initial value for the optimizer. The optimization is faster if this value already respects the constraints, i.e. the point is already in all light cones.
A simple way to have one is to take a point far in the future.
x0 = satelittes[0].copy()
x0[-1] = c * (100 + max(abs(s[-1]) for s in satelittes))
x0
Now, we can optimize:
from scipy.optimize import minimize
result = minimize(cost, x0=x0, constraints=constraints)
x0, t0 = result.x[:-1], result.x[-1]
Final thought
This optimization problem is only one possibility to find a position using GNSS. I don't know how it is done in real life and there may be easier way to solve this problem.
Category: maths Tagged: python maths optimization