Zombie propagation

Sat 21 March 2020

Zombie favorite food warning (Photo credit: wikipedia)

I recently read a paper [1] trying to model a disease propagation. I wanted to play with this model.

The model

The model is know as "SIR" as it divide the population into 3 groups:

S: suceptible to become a zombie
I: infected, and thus zombified
R: recovered, and (hopefully) immune

It then model the move of individuals between groups. The principle of dividing a population into such group and modeling the transitions of individual is known as a compartmental model and many results have already been published about such models. I won't insist on the \(R_0\) (basic reproduction number).

For fun, and because it is already done by scientific researchers, I will add other groups:

Q: quarantined
D: dead
AC: asymptomatic carrier (exposed, can infect other but not zombified)

I'll use the follwing transition between groups:

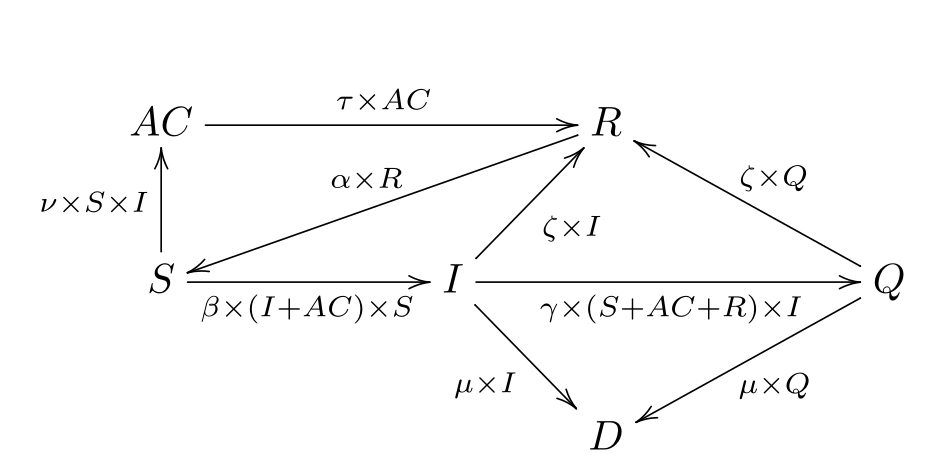
Zombie transition diagram

Note that:

this is only a toy model
transitions rates are proportional to population of some groups (more zombies and more suceptibles \(\implies\) more mettings between both groups, zombies can be put in quarantine faster if there is more non-zombie able to do it)
\(\zeta = \frac{1}{\lambda}\) in some research paper, \(\lambda\) being a recovery time.
only zombie can die, e.i. other death causes are not modeled
once recovered, there is a slight chance to not be immune (model either mutation in the desease or people needing a booster shot)

This model is thus entirely described by the following equations:

\begin{equation*} \begin{cases} \frac{\partial{S}}{\partial{t}} &= - \nu S(t) I(t) + \alpha R(t) - \beta (I(t) + AC(t)) \times S(t)\\ \frac{\partial{I}}{\partial{t}} &= \beta (I(t) + AC(t)) \times S(t) - \zeta I(t) - \gamma (S(t) + AC(t) + R(t)) \times I(t) - \mu I(t)\\ \frac{\partial{R}}{\partial{t}} &= \zeta (I(t) + Q(t)) + \tau AC(t) - \alpha R(t)\\ \frac{\partial{Q}}{\partial{t}} &= \gamma (S(t) + AC(t) + R(t)) \times I(t) - (\mu + \zeta) Q(t)\\ \frac{\partial{D}}{\partial{t}} &= \mu(I(t) + Q(t))\\ \frac{\partial{AC}}{\partial{t}} &= \nu S(t) I(t) - \tau AC(t) \end{cases} \end{equation*}

The game

I use python to code this model. I use scipy.integrate.odeint. I simulated some scenarii [2]

This model clearly needs improvements (quarantine is useless in this model). In this model the asymptomous carrier, even if they are few, can have a visible influence on the outcome.

We can now collect possible outcomes:

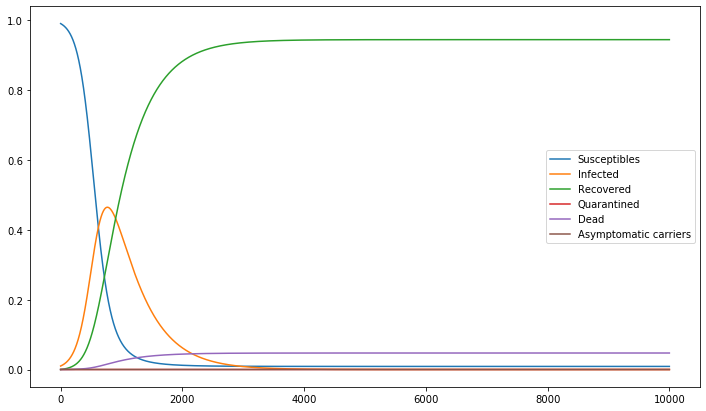
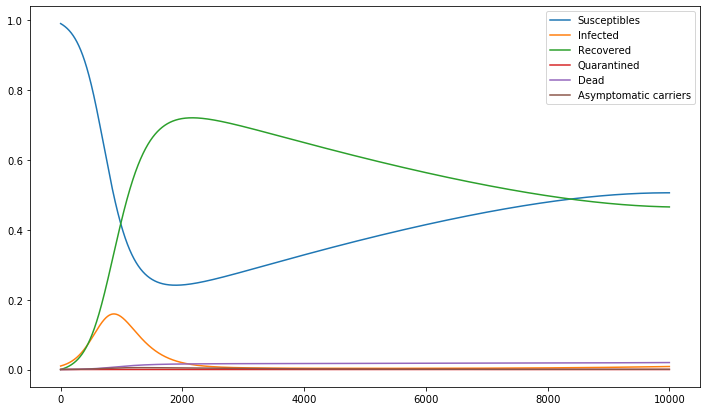
[1]	C Witkowski and B Blais (2013), "Bayesian analysis of epidemics-zombies, influenza, and other diseases"

[2]	a jupyter notebook containing my code is available here (also in pdf)